Pollard Rho Algorithm Study

Lyutoon

cryptographyalgorithm

发布于：2020年11月18日

次浏览

一、引言

在上一篇博客中,我们了解了Pollard p-1 算法,这次,请随我看看另一个名叫Pollard Rho的算法又能对大整数分解问题提供什么帮助吧！不过同样的,大整数分解问题在因子选取得当的情况下,要想解决它是极为困难的,因此,Pollard Rho也有它自己的适用条件,下面,我们开始正式介绍这个未曾谋面的算法吧！

二、Pollard Rho算法

(1) 适用条件

Pollard Rho算法可以分解大整数是基于大整数$n=pq$中$p$和$q$之间有一个因子很小,在此情况下,我们可以利用该算法完成对$n$的分解。

(2) 基本思想

Pollard Rho算法其实是基于寻找指定哈希函数的碰撞的思想才设计的算法。如果我们可以找到不相等的$x$和$x’$并且使得：

那么我们就可以知道$x$和$x’$其实相差$p$的整数倍,由此我们可以知道$gcd(x-x’,n)$如果不是$1$也不是$n$,那么我们就成功分解了。

(3) 具体原理

首先我们先了解一下密码学中一个对哈希函数的经典攻击方式:生日攻击,其主要原理是生日悖论。(在此先简单介绍一下,以后会出一篇专门的文章来记录这个方法)

生日悖论：如果一个房间里有n个人,那么在不考虑特殊因素的前提下,例如闰年、双胞胎,假设一年365日出生概率是平均分布的,需要多少个人才可以保证在这n个人中有50%的概率出现两个人生日相同呢？答案是n=23。更有趣的是当n=57的时候这个概率竟然高达99%。有兴趣的朋友可以了解一下具体的证明,涉及到简单的概率论知识。
生日攻击：生日攻击是基于生日悖论问题的扩展版本,考虑一个值域有n个元素的哈希函数h(x),那么利用与推导生日悖论相似的方法,我们可以得出,如果要使此哈希函数有至少50%的概率产生碰撞,则大约需要1.17$\sqrt n$次不同的x的尝试。

我们考虑一个哈希函数$h:\left\{0,1,\dots,n-1\right\}\rightarrow \left\{0,1,\dots,p-1\right\}$,定义为$h(x)=x\,mod\,p$.

那么我们由生日悖论可以知道我们如果随意选择$X\subseteq \left\{0,1,\dots,n-1\right\}$,$|X|=1.17\sqrt p$则有：

但是,我们对这个算法进行分析的话,可以发现,如果我们用简单的$h(x)=x\,mod\,p$作为哈希函数,则要计算$\dbinom{|X|}{2}>\frac{p}{2}$次$gcd(x,x’)$才可以找到这个公因数,复杂度太高了(甚至要比遍历$n$的复杂度还高2333)。因此我们要设计一个比较合理的哈希函数来降低这个复杂度。

考虑一个多项式函数$f(x)=x^2+a$,在Pollard Rho算法中,$a$通常取为$1$。我们假设映射$x\mapsto f(x)\,mod\,p$表现得像一个随机映射(事实上在大多数时候就是表现得像随机映射),主要是为了使这个算法获得的值更加均匀,防止出现像$h(x)$一样的那种遍历式复杂度,同时也可以使这个哈希函数更加像一个$oracle\,\,modle$,这样才可以使生日攻击更有效。令$x_1\in\mathbb{Z_n}$,考虑一个序列$x_1,x_2,\dots,$满足：

而我们就是要在这个序列中找到$x_i,x_j\,s.t.\,gcd(x_i-x_j,n)>1$.

假设$x_i\equiv x_j\,mod\,p$,那么${x_i}^2+1\equiv {x_j}^2+1\,mod\,p$,而$x_{i+1}=f(x_i)$,因此,我们可以推断出$x_{i+1}\equiv x_{j+1}\,mod\,p$,一直这样递推下去那么我们可以得到结论：

我们令$l=j-i$,那么就有:如果$j’>i’\ge i$并且$j’-i’$是$l$的整数倍,那么就会得到$x_{i’}\equiv x_{j’}\,mod\,p$。

画成图形大概长这样：

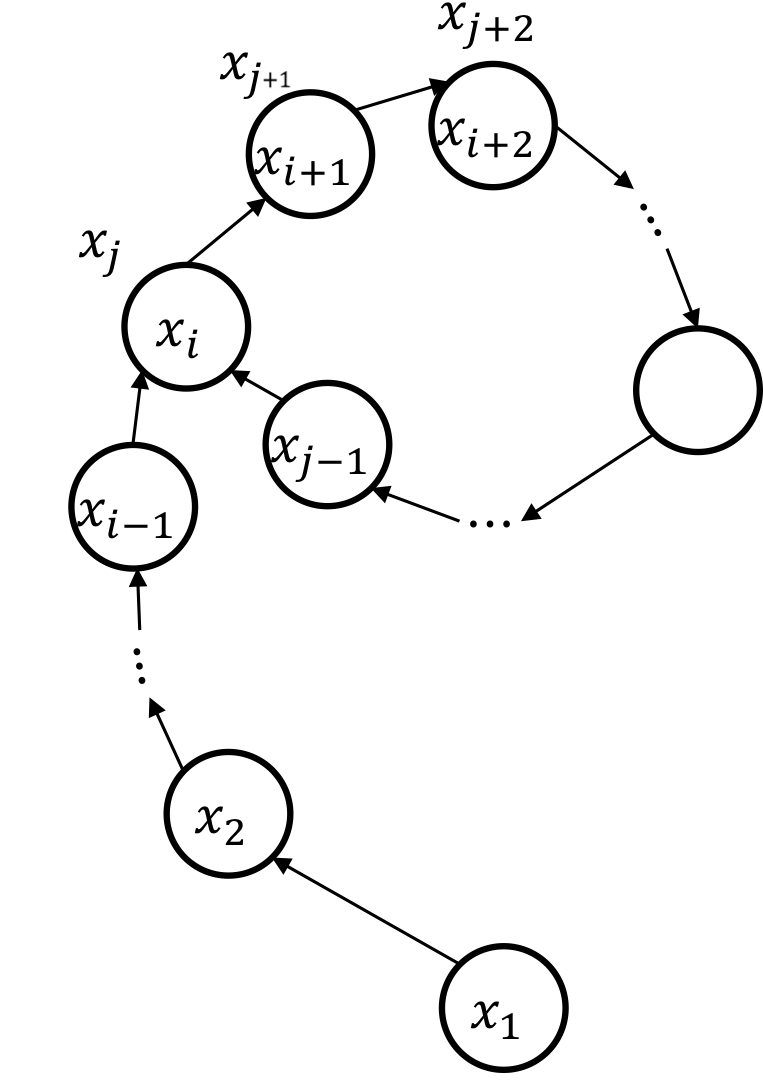
因为长得比较像希腊字母$\rho$(Rho),因此得名Pollard Rho。

那么我们知道了这些原理,又怎么来找这个$i$和$j$呢？这时候我们可以想,既然里面有一个环,我们是不是可以用弗洛伊德判环法来找出$i$和$j$。那么什么是弗洛伊德判环法呢？

其实弗洛伊德判环法有点类似于追及问题的一个算法,我们想象一下有两个人在环形操场赛跑,一个人速度是$v$,另一个是$2v$,那么总有一天速度快的那个人要追上速度慢的那个人,并且此时超过了慢速的人一圈。弗洛伊德判环法就是利用了这个性质设计的。

在此处,我们令一个$x$每次套上一层$f(x)$,另一个$x$每次套上两层$f(x)$。举个例子,如果从$x_0$开始,那么慢的那个下一次应该是$f(x_0)\,mod\,n=x_1$,而快的那个则是$f(f(x_0))=x_2$这样子。也就是说$x_{快}=2x_{慢}$。

这样一来如果我们在这个追及过程中出现了$gcd(x_{快}-x_{慢},n)\notin\left\{1,n\right\}$,则分解成功，找,了$p$。

整个代码的复杂度为$O(n^{1/4})$

(4) 伪代码和代码实现

伪代码：

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

from libnum import *
from Crypto.Util.number import *

def Pollard_Rho(n):
    f = lambda x: (x*x + 1) % n
    x = 2
    _x = f(x)
    p = gcd(x - _x, n)
    while p == 1:
        x = f(x)
        _x = f(f(_x))
        p = gcd(x - _x, n)
    if p == n:
        print('[+] Failed')
    else:
        print('[+] Done! Find p:', p)
        print('[+] n =', p, '*', n//p)
        return p

p = getPrime(20)
n = p * getPrime(1024)
Pollard_Rho(n)

"""
output:
[+] Done! Find p: 1003507
[+] n = 1003507 * 119194734255586430249491786028030901955714303727483782260194798985850318067046294210092944971608413702515710726741826459609793866216394194576322278249676418761626477844699560122695407656121947507162012151299590017153791311273871754406254980031843483910743861839907953660598736617115028062045825098452377479049
"""

因为$p$实在是太小了,整个代码跑起来差不多1s。但是python跑的有点慢,用C的话会快好多。因此我们可以看出如果一个大整数中有较小的素数,我们都可以很快地将其分解出来。

三、结语

通过这个算法,告诫我们在RSA等依赖大整数分解困难性的加密系统选取大整数的时候,两个素数不要相差太远,因为1024bit和1024bit是不一样的,同样是1024bit尽量选取同样比特的$pq$效果会更好,不要一个很大一个很小,这样可以有效抵御Pollard Rho算法的攻击。

感谢大家看到这里,今后我还会更新一些有趣的密码学中的算法,希望可以让大家收获知识和乐趣！

更新于：2021年4月22日